Loading... # 简单排序二分法与异或运算 ## 排序 ### 选择排序 假设有一个长度为N的数组,选择排序的过程就是,从0~N-1中选出最小值,与0位置交换,再从1\~N-1中选出最小值与1位置交换,再从2\~N-1中选出最小值,与2位置交换,以此类推直到N-2\~N-1结束。 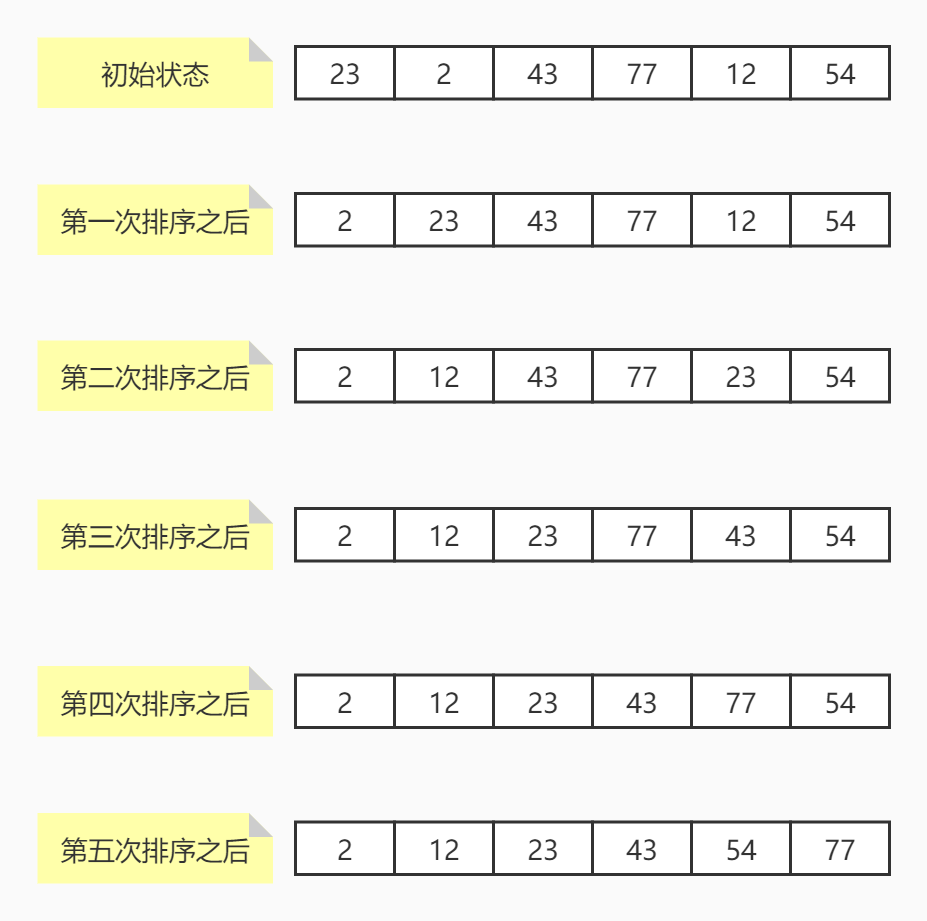 #### 代码实现 ```java public static void sort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 0; i < arr.length; i++) { int min = i; for (int j = i + 1; j < arr.length; j++) { min = arr[min] < arr[j] ? min : j; } swap(arr, i, min); } } ``` ### 冒泡排序 假设有一个长度为N的数组,先比较0位置和1位置,如果0位置比1位置大,就进行交换,然后再比较1位置和2位置,2位置和3位置,一直比较到N-2位置与N-1位置,这时,可以保证最大的数被移动到了最右边。然后再次比较0位置与1位置,1位置与2位置,一直比较到N-3位置与N-2位置,因为N-1在上一次比较已经最大,这次不用比较,经过该次比较可以保证第二大的被移动到了N-2的位置上,周而复始,直到只需要比较1位置和2位置为止。该算法会将元素像气泡一样推到最右边并且越来越大,所以叫冒泡排序。 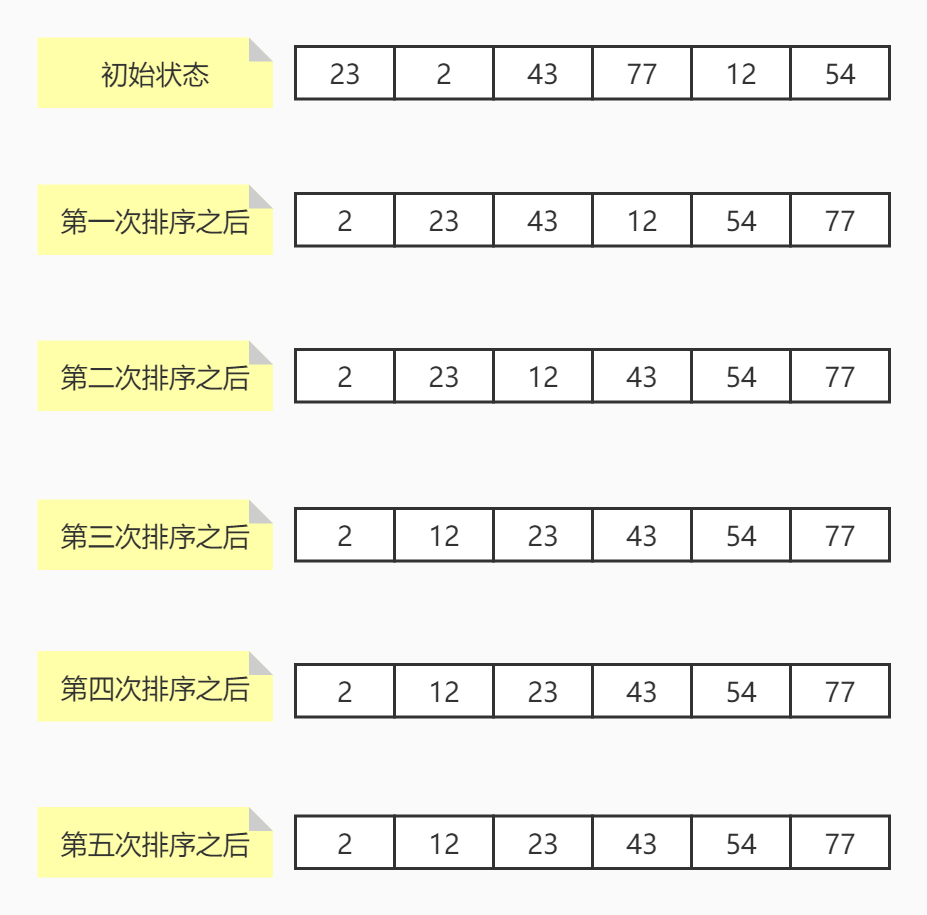 #### 代码实现 ```java public static void sort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = arr.length - 1; i > 0; i--) { for (int j = 0; j < i; j++) { if (arr[j] > arr[j + 1]) { swap(arr, j, j + 1); } } } } ``` ### 插入排序 插入排序是从0位置为开始,第一次比较1位置是否比0位置小,如果小就交换,第二次到2位置,从2位置向左看,如果2比1小,就交换,然后再比较0位置和1位置。第三次到3位置,从3位置向左看,比较3位置和2位置,2位置和1位置,1位置和0位置。以此类推,就向打扑克牌时,整理手牌顺序一样。 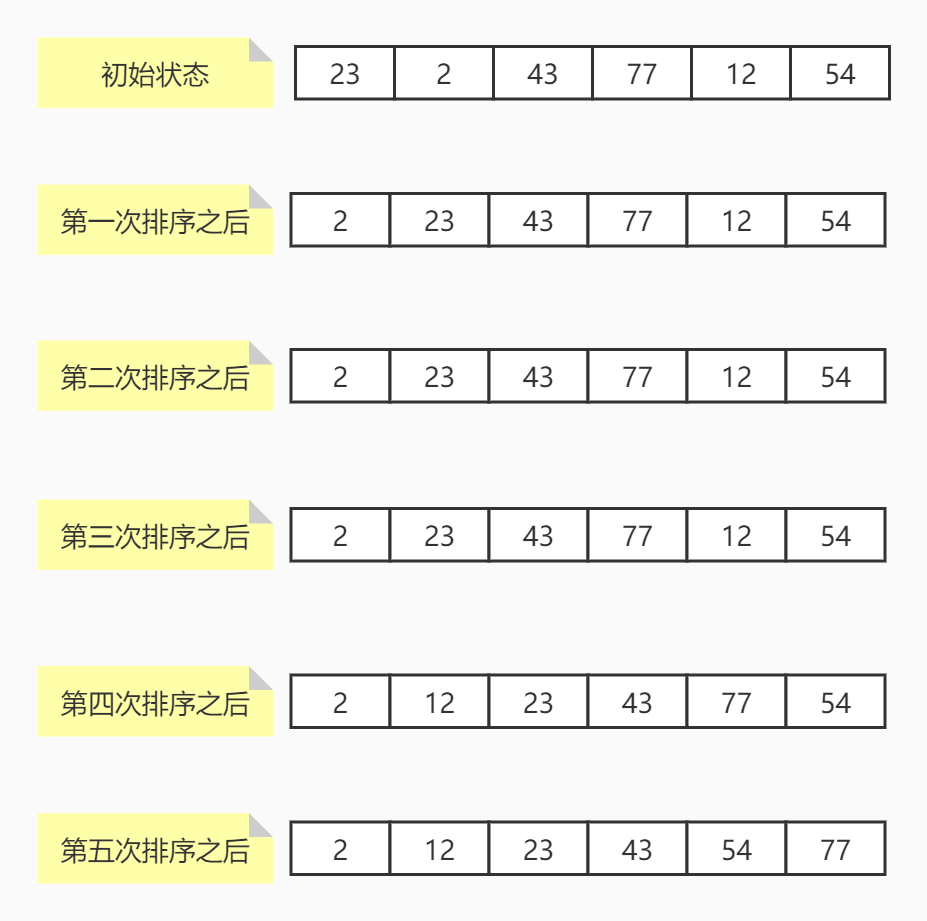 #### 代码实现 ```java public static void sort(int[] arr) { if (arr == null || arr.length < 2) { return; } for (int i = 1; i < arr.length; i++) { for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) { swap(arr, j, j + 1); } } } ``` ## 二分法 ### 二分查找 针对有序数组中需要找到是否存在某个值,可以找到该数组的中间位置,判断是否比该值大,如果大于该值,说明要去左边的一半找,否则去右边的一半找,确定好在哪一边后,再进行二分,再次比较,直到中间值等于该值或者没有找到结束。 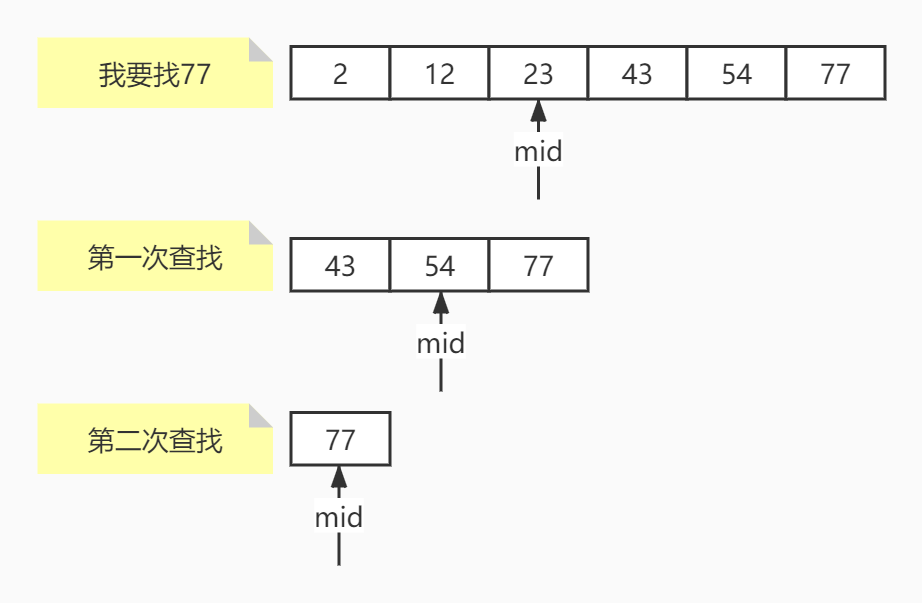 #### 代码实现 ```java public static int indexOf(int[] arr, int value) { int left = 0; int right = arr.length - 1; while (left <= right) { int mid = left + ((right - left) >> 1); if (arr[mid] < value) { left = mid + 1; } else if (arr[mid] > value) { right = mid - 1; } else { return mid; } } return -1; } ``` ### 查找大于等于查找值最左侧的值 先进行二分,如果mid的值大于等于要查找的值,则向左继续查找,否则向右查找,直到无法再进行分割为止。 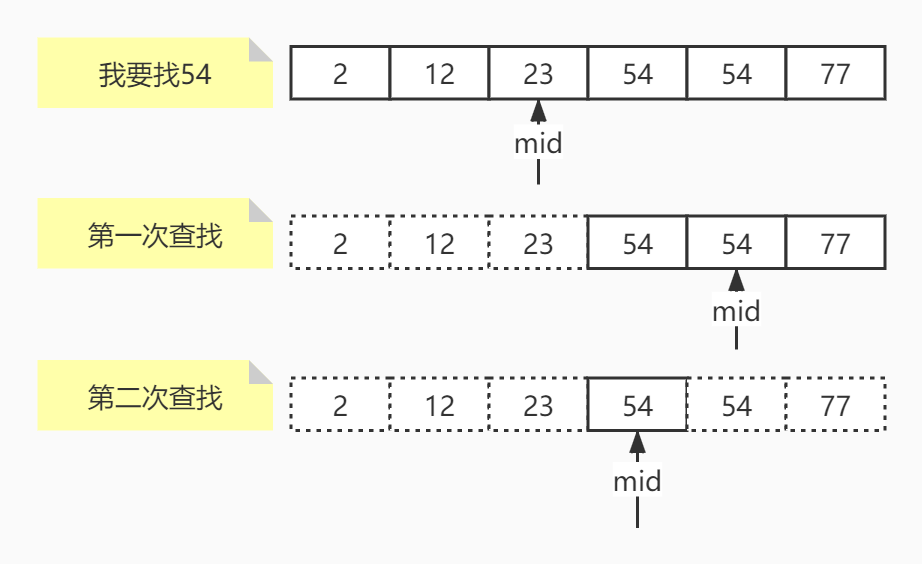 #### 代码实现 ```java public static int indexOf(int[] arr, int value) { int left = 0; int right = arr.length - 1; int index = -1; while (left <= right) { int mid = left + ((right - left) >> 1); if (arr[mid] >= value) { index = mid; right = mid - 1; } else { left = mid + 1; } } return index; } ``` ### 局部最小值 什么是局部最小值? 如果有一个长度为N的数组: - 在0位置,如果它比1位置值小,那么它就是局部最小值。 - 在N-1位置,如果它比N-2位置值小,那么它就是局部最小值。 - 其它位置i,满足i位置同时比i-1位置与i+1位置小,那么它就是局部最小值。 设计一个算法,找出数组中任意一个局部最小值。数组中任意两个相邻的数都不相等,数组无序。 看到无序,可以用二分法吗?答案是可以的,如下图: 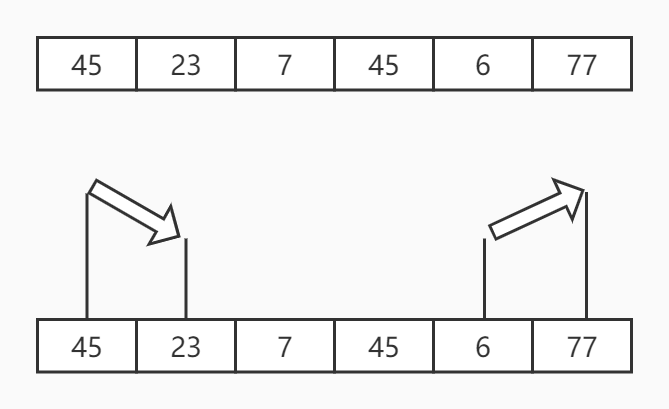 虽然数组整体无序,但是它有一个下降到上升的趋势,如果要想实现该趋势,那么在下降到上升之间必定存在局部最小值(无论怎么连线)。对该数组进行二分法,判断中间值左右的值是否比它大,如果都比它大,那么它就是局部最小值。反之,肯定至少有一个比它小,向任意一个比它小的方向继续二分,再次比较,以此类推。为什么我们可以使用二分?我们根据趋势,可以判断,在小的那一边,必定存在局部最小值,当然在大的那一边也可能存在,我们只需要找出其中一个,所以可以放弃大的一边。在明确的知道可以合理排除掉另一半数据的时候,无论数组有没有序,都可以使用二分法。 #### 代码实现 ```java public static int min(int[] arr) { if (arr == null || arr.length == 0) { return -1; } if (arr.length == 1 | arr[0] < arr[1]) { return 0; } if (arr[arr.length - 1] < arr[arr.length - 2]) { return arr.length - 1; } int left = 1; int right = arr.length - 2; while (left <= right) { int mid = left + ((right - left) >> 1); if (arr[mid] > arr[mid - 1]) { right = mid - 1; } else if (arr[mid] > arr[mid + 1]) { left = mid + 1; } else { return mid; } } return left; } ``` ## 异或运算 异或运算是一种二进制运算,两个二进制数做异或,每个二进制位如果相同异或结果为0,不同异或结果为1。区别于同或,相同为1,不同为0。 异或满足下列性质: - 0^N=N - N^N=0 - 满足交换律与结合律(一堆数做异或结果与顺序无关) 根据以上性质,可以做什么操作呢? 最简单的,不创建临时变量交换两个数a、b的值。 ```java int a = 3; int b = 6; a = a ^ b; b = a ^ b; a = a ^ b; ``` 我们分析一下上面代码的执行过程: 1. `a = a ^ b;`执行完该操作后,`a=3^6`,`b=6`。 2. `b = a ^ b;`执行完该操作后,`a=3^6`,`b=3^6^6`,根据N^N=0与结合律,`b=3^0`,根据0^N=N,`b=3`。 3. `a = a ^ b;`执行完该操作后,`a=3^6^3`,`b=3`,同上,`a=3^6^3`也就是`a=6`。 问题1:数组中,某一种元素有奇数个,其它元素的数量都是偶数个,获取数量为奇数个的元素。 ```java public static void printOddTimesNum1(int[] arr) { int eor = 0; for (int i : arr) { eor ^= i; } System.out.println(eor); } ``` 初始化eor为0,然后用eor与数组中所有元素做异或,最后的值就是奇数个数元素的值。N^N=0,也就是说,所有偶数个数的元素异或完的值都是0,0^N=N,最后只剩下一个奇数个数的元素。 问题2:如果有两种元素都是奇数个,其它都是偶数个,求这两种元素的值。 **补充知识**:获取二进制最右边的1 ```java eor & (~eor + 1); ``` 就是该值与上该值取反加1的和。一个值与上自己的反码肯定是0,加1操作就是通过进位,把最右边的1推过去,这样,与操作时就能留下最右边的1。  首先,我们依然初始化eor为0,然后让eor与数组中每个元素做异或,我们假设这两种数量为奇数的元素值分别为a、b,那么可以肯定,最后eor一定等于a^b。因为a!=b,也就是a^b!=0,因此,eor的值的某一位肯定是有1的,有1就说明,a与b这一位的值不同。因此我们可以根据这一位的值,把数组中的元素分成两拨,为1的一拨为0的一拨。我们可以肯定的是,a与b一定不在同一拨,但是这对其他元素在每一拨中奇偶的个数没有影响。我们再初始化一个eor'=0,这个eor'去与其中一拨的每一个元素做异或,最后的值就是a与b其中的一个,然后再用该值异或上eor,就得到了另一个。至于根据哪一位分拨,就选择最右边的1,也就是我们上边提到的算法。 ```java public static void printOddTimesNum2(int[] arr) { int eor = 0; for (int i : arr) { eor ^= i; } int rightOne = eor & (~eor + 1); int newEor = 0; // eor' for (int i : arr) { if ((i & rightOne) != 0) { newEor ^= i; } } System.out.println(newEor + " " + (eor ^ newEor)); } ``` Last modification:November 28th, 2020 at 11:47 pm © 允许规范转载